Віднімання дробів із однаковими знаменниками – це простий і захопливий процес, який може здатися складним лише на перший погляд. Уявіть: ви ділите смачний пиріг, і потрібно знати, скільки залишиться, якщо від цілого відріжете шматочок. Саме так працюють дроби – і ми розберемо це по полицях!
Ця навичка стане в пригоді не лише в школі, а й у житті – від готування до розрахунків. У статті ми детально пояснимо, як віднімати дроби з однаковими знаменниками, додамо приклади й підкажемо, як уникнути помилок. Готові зануритися в світ математики легко й із задоволенням? Тоді вперед!
Що таке дроби з однаковими знаменниками
Перш ніж учитися віднімати, давайте розберемося, що таке дроби з однаковими знаменниками. Дріб – це число, яке показує частину цілого, наприклад, 1/4 чи 3/5. Воно складається з чисельника (верхня частина) і знаменника (нижня частина).
Одинакові знаменники означають, що нижні числа в дробах однакові – наприклад, 2/5 і 3/5. Це як два шматки пирога, розрізані на однакову кількість частин (по 5), але з різною кількістю взятих шматочків (2 і 3). Такі дроби віднімати легко – і зараз ви дізнаєтеся як!
Головне – зрозуміти, що знаменник показує, на скільки частин поділили ціле, а чисельник – скільки із них узяли. Якщо знаменники збігаються, усе просто!
Чому знаменники важливі
Ось ключові моменти про дроби з однаковими знаменниками:
- Один розмір частин. Знаменник визначає розмір кожної частинки – якщо він однаковий, частинки однакові.
- Спрощення. Одинакові знаменники дозволяють працювати лише з чисельниками, не чіпаючи низ.
- Логіка. Це як відняти 2 яблука від 3, коли всі яблука однакові за розміром.
Знаючи це, ви вже на півдорозі до успіху. Тепер до самої дії!
Як віднімати дроби з однаковими знаменниками: правило
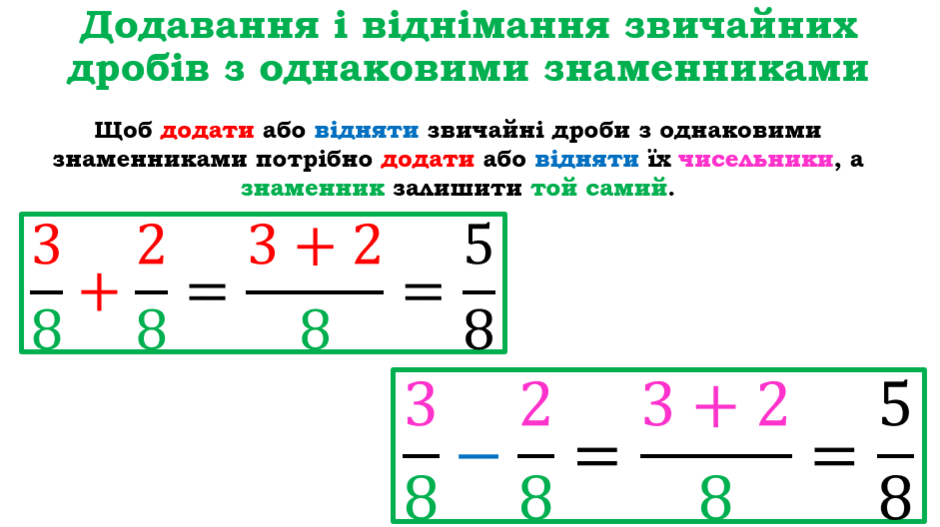
Віднімати дроби з однаковими знаменниками – це простіше, ніж здається. Основне правило: віднімайте чисельники, а знаменник залишайте без змін. Звучить легко? Так і є!
Наприклад, візьмемо 5/7 – 2/7. Тут від 5 (чисельник першого дробу) віднімаємо 2 (чисельник другого дробу), а 7 (знаменник) лишаємо як є. Отримуємо 3/7 – і все готово!
Це працює, бо знаменник показує розмір частин, а нам треба лише порахувати, скільки їх залишиться. Усе логічно й швидко – головне, не плутати верх і низ!
Покрокова інструкція віднімання
Ось як це зробити крок за кроком:
- Перевірте знаменники. Упевніться, що вони однакові – наприклад, 4/9 і 2/9.
- Відніміть чисельники. Від першого чисельника (4) відніміть другий (2) – вийде 2.
- Залиште знаменник. Знаменник (9) не змінюється – результат 2/9.
- Перевірте. Усе просто, але переконайтеся, що не помилилися в обчисленнях.
Ця схема – ваш надійний помічник. Спробуйте, і переконаєтеся, що це як гра!
Приклади віднімання дробів
Теорія – це добре, але приклади – краще. Давайте розберемо, як віднімати дроби з однаковими знаменниками на практиці. Це закріпить правило й додасть упевненості.
Приклад 1: 3/4 – 1/4. Знаменники однакові (4), віднімаємо чисельники: 3 – 1 = 2. Результат – 2/4. Можна скоротити до 1/2, але про це пізніше.
Приклад 2: 7/10 – 4/10. Знову однакові знаменники (10), віднімаємо: 7 – 4 = 3. Отже, 3/10 – усе чисто й просто!
Ще кілька прикладів для практики
Спробуйте самі:
- 5/8 – 2/8. Віднімаємо: 5 – 2 = 3, результат – 3/8.
- 9/12 – 7/12. Рахуємо: 9 – 7 = 2, отримуємо 2/12 (можна скоротити до 1/6).
- 4/5 – 3/5. Віднімаємо: 4 – 3 = 1, результат – 1/5.
Бачите, як усе легко? Приклади – це ваш тренажер для математики!
Що робити, якщо результат від’ємний
Іноді при відніманні чисельник може стати від’ємним – наприклад, 2/7 – 5/7. Як віднімати дроби з однаковими знаменниками в такому разі? Не панікуйте – це можливо!
Рахуємо як завжди: 2 – 5 = -3. Отже, результат – -3/7. Від’ємний дріб означає, що ми “забрали більше, ніж мали” – це нормально в математиці, хоч і рідко буває в реальному житті.
Якщо завдання шкільне, перевірте умову – можливо, ви помилилися в порядку дробів. Але правило те саме: віднімайте чисельники, знаменник не чіпайте.
Як працювати з від’ємними дробами
Ось що важливо:
- Просто віднімайте. 3/10 – 7/10 = -4/10 (можна скоротити до -2/5).
- Перевірте логіку. Якщо результат нелогічний (наприклад, “залишилося -2 шматки”), перегляньте задачу.
- Зберігайте знак. Від’ємне число – це нормально, не ігноруйте мінус.
Від’ємні дроби – не страшно. Головне – уважність і правильний розрахунок!
Скорочення дробів після віднімання
Після віднімання дробів із однаковими знаменниками іноді можна скоротити результат. Що це означає? Якщо чисельник і знаменник мають спільний дільник, дріб спрощується – стає “красивішим”.
Наприклад, 4/8 – 2/8 = 2/8. Число 2 і 8 діляться на 2: 2 ÷ 2 = 1, 8 ÷ 2 = 4. Отже, 2/8 = 1/4. Скорочення не обов’язкове, але робить відповідь елегантною.
Перевіряйте завжди: якщо є спільні дільники (2, 3, 5 тощо), діліть обидва числа. Але тільки після віднімання!
Як скоротити дріб
Ось як це зробити:
- Знайдіть дільник. Подивіться, на що діляться чисельник і знаменник – наприклад, 6/12 (обидва на 6).
- Поділіть. 6 ÷ 6 = 1, 12 ÷ 6 = 2, отримуємо 1/2.
- Перевірте. Скоротили правильно? Помножте назад – має вийти початковий дріб.
Скорочення – це “полірування” вашої відповіді. Воно додає акуратності!
Таблиця: приклади віднімання дробів
Щоб усе стало ще зрозуміліше, ось таблиця з прикладами віднімання дробів із однаковими знаменниками:
| Приклад | Віднімання | Результат | Скорочений результат |
|---|---|---|---|
| 3/4 – 1/4 | 3 – 1 = 2 | 2/4 | 1/2 |
| 7/10 – 2/10 | 7 – 2 = 5 | 5/10 | 1/2 |
| 5/6 – 4/6 | 5 – 4 = 1 | 1/6 | – |
| 2/5 – 3/5 | 2 – 3 = -1 | -1/5 | – |
Ця таблиця – ваш швидкий довідник. Користуйтеся, щоб перевірити себе!
Чого уникати при відніманні дробів
Віднімати дроби з однаковими знаменниками легко, але помилки трапляються. Щоб правильно це зробити, знайте, де можна оступитися. Увага до деталей – ваш найкращий друг!
Не віднімайте знаменники – це найпоширеніша помилка новачків. Наприклад, 5/7 – 2/7 не дорівнює 3/5 – знаменник не чіпаємо! І не забувайте перевіряти, чи однакові знаменники – якщо ні, це вже інша історія.
Ще одна пастка – поспішні обчислення. Порахуйте спокійно, щоб не отримати 4 замість 3. Математика любить точність!
Типові помилки при відніманні
Ось що може піти не так:
- Віднімання знаменників. 3/8 – 1/8 ≠ 2/7 – низ лишається той самий!
- Плутанина з чисельниками. 6/9 – 4/9 = 2/9, а не 3/9 – перевіряйте арифметику.
- Ігнор знаків. 2/5 – 3/5 = -1/5, а не 1/5 – мінус важливий.
Уникайте цих підводних каменів, і ваші дроби будуть бездоганними!
Як перевірити правильність віднімання
Закінчили віднімати дроби з однаковими знаменниками? Перевірте себе – це займе секунду, але врятує від помилок. Є простий спосіб переконатися, що все правильно.
Додайте результат до віднятого дробу – має вийти початкове число. Наприклад, 5/7 – 2/7 = 3/7. Перевіряємо: 3/7 + 2/7 = 5/7. Усе зійшлося – значить, усе гаразд!
Ще можна уявити це як частини пирога: від 5 шматків із 7 відняли 2 – лишилося 3. Логіка й арифметика мають співпадати!
Методи перевірки
Ось як упевнитися в результаті:
- Додавання назад. 4/6 – 1/6 = 3/6, перевірка: 3/6 + 1/6 = 4/6 – працює!
- Малюнок. Намалюйте дріб (коло, поділене на частини) – візуально легше зрозуміти.
- Калькулятор. Уведіть дроби – сучасний спосіб для лінивих.
Перевірка – це ваша страховка. Дроби люблять точність, тож не лінуйтеся!
Практичне застосування в житті
Віднімати дроби з однаковими знаменниками – це не просто шкільна вправа, а корисна навичка. Уявіть: ви печете торт і маєте 3/4 склянки цукру, а рецепт просить 1/4 – скільки лишиться? Або будуєте полицю й відрізаєте 2/5 метра від 4/5.
У повсякденні дроби з однаковими знаменниками трапляються частіше, ніж здається – у рецептах, бюджетах, вимірах. Знати, як їх віднімати, – це як мати суперсилу для практичних завдань!
Тож наступного разу, коли будете ділити пиріг чи фарбу, згадайте це правило – і все вийде як по маслу!