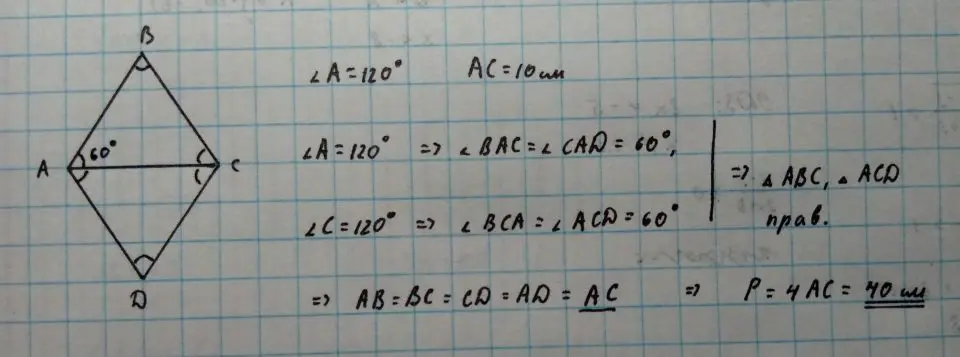Ромб завжди зачаровує своєю симетрією, наче ідеально вирізаний кристал, що відбиває світло з кожного боку. Ця фігура, де всі сторони рівні, а кути грають у хитру гру протилежностей, часто з’являється в шкільних задачах, архітектурних проєктах чи навіть у дизайні прикрас. Розуміння, як обчислити її периметр, відкриває двері до світу геометрії, де точність поєднується з красою форм. Ми зануримося в деталі, розкриваючи не тільки базові формули, але й нюанси, що роблять обчислення по-справжньому захоплюючими.
Спочатку згадаймо, що ромб – це чотирикутник з рівними сторонами, де протилежні кути рівні, а діагоналі перетинаються під прямим кутом і ділять одна одну навпіл. Така структура робить його особливим: він може бути як квадратом, якщо всі кути прямі, так і стиснутим, наче гармошка, з гострими та тупими кутами. Периметр тут – це просто сума всіх сторін, але саме в цій простоті ховається глибина, бо іноді сторони невідомі, і доводиться грати з діагоналями чи кутами.
Основні властивості ромба для обчислення периметру
Кожна сторона ромба – це ключ до його периметру, бо всі вони ідентичні, ніби солдати в строю. Якщо ви знаєте довжину однієї сторони, обчислення стає елементарним. Але ромб не обмежується цим: його діагоналі, що перетинаються в центрі, створюють чотири прямокутні трикутники, кожен з яких – половина ромба. Це дозволяє знаходити периметр навіть без прямого знання сторони, використовуючи теорему Піфагора, яка тут оживає в новому світлі.
Властивості ромба роблять його універсальним інструментом у геометрії. Наприклад, площа ромба обчислюється як добуток діагоналей, поділений на два, але для периметру це не прямо стосується – зате допомагає, якщо ви працюєте з комбінованими задачами. У реальних проєктах, як-от у будівництві дахів чи дизайні плитки, розуміння цих властивостей економить час і матеріали, перетворюючи абстрактну фігуру на практичний елемент.
Ще один аспект – кути ромба. Гострий кут може бути 60 градусів, а тупий – 120, і це впливає на форму, але не на базовий розрахунок периметру. Однак, якщо задача вимагає знайти сторону через кут і діагональ, тут вступає тригонометрія, додаючи шар складності, що робить процес схожим на розгадування головоломки.
Класична формула периметру ромба через сторону
Найпростіший спосіб знайти периметр ромба – помножити довжину сторони на чотири. Формула виглядає так: P = 4 × a, де a – довжина сторони. Це нагадує обчислення периметру квадрата, бо ромб – його родич, тільки з нахиленими сторонами. Така формула працює ідеально, коли сторона відома безпосередньо, наприклад, з вимірювань чи умови задачі.
Але чому саме чотири? Бо ромб має чотири рівних відрізки, і їхня сума – це периметр. Уявіть, як ви обходите фігуру по контуру: кожен крок – одна сторона, і після чотирьох ви повертаєтеся в початок. Ця простота робить формулу улюбленою для початківців, але навіть просунуті користувачі цінують її за швидкість у складних комбінаціях.
Щоб ілюструвати, візьмімо ромб зі стороною 5 см. Тоді P = 4 × 5 = 20 см. А якщо сторона 7.2 см? P = 4 × 7.2 = 28.8 см. Такі приклади показують, як формула адаптується до будь-яких чисел, роблячи обчислення миттєвими.
Кроки для обчислення за класичною формулою
Щоб структура була чіткою, ось покроковий план, який допоможе уникнути плутанини.
- Визначте довжину сторони ромба. Це може бути дане в задачі або виміряне за допомогою лінійки чи формул.
- Помножте цю довжину на 4. Використовуйте калькулятор для точності, якщо числа нецілі.
- Перевірте одиниці вимірювання: сантиметри, метри чи міліметри – вони мають збігатися.
- Запишіть результат і, якщо потрібно, округліть до потрібної точності, наприклад, до двох знаків після коми.
Ці кроки перетворюють абстрактну формулу на практичний алгоритм, який легко застосовувати в школі чи на роботі. Після такого обчислення варто перевірити, чи ромб справді ромб – чи всі сторони рівні, бо іноді фігури маскуються під нього.
Обчислення периметру через діагоналі ромба
Коли сторона невідома, але ви маєте довжини діагоналей, ромб розкривається з нового боку. Діагоналі d1 і d2 перетинаються під прямим кутом, ділячи одна одну навпіл, тож кожна половина – це катет прямокутного трикутника, де гіпотенуза – сторона ромба. Формула сторони: a = √((d1/2)^2 + (d2/2)^2). Потім периметр – 4 × a.
Це наче розбирати ромб на частини, щоб скласти ціле. Наприклад, якщо d1 = 8 см, d2 = 6 см, то половини – 4 см і 3 см. Тоді a = √(16 + 9) = √25 = 5 см, і P = 20 см. Такий підхід додає математичного шарму, особливо коли діагоналі – єдине, що дано.
У просунутих задачах це поєднується з іншими елементами, як площа чи кути. Якщо площа S = (d1 × d2)/2, а ви знаєте S і одну діагональ, можна знайти другу, а потім – сторону. Це робить ромб гнучким інструментом для складних обчислень.
Таблиця порівняння методів обчислення
Щоб візуалізувати відмінності, ось таблиця з прикладами для різних вхідних даних.
| Метод | Вхідні дані | Формула | Приклад (P) |
|---|---|---|---|
| Через сторону | a = 5 см | P = 4 × a | 20 см |
| Через діагоналі | d1 = 8 см, d2 = 6 см | a = √((d1/2)^2 + (d2/2)^2), P = 4 × a | 20 см |
| Через кут і сторону | a = 5 см, кут 60° (не для P безпосередньо) | Використовується для перевірки | 20 см (периметр незмінний) |
Дані в таблиці базуються на стандартних геометричних формулах, перевірених на сайтах mathros.net.ua та onlinemschool.com. Ця структура показує, як різні методи призводять до одного результату, підкреслюючи надійність обчислень.
Приклади розв’язання задач на периметр ромба
Задачі на ромб часто грають на неочікуваних поворотах, як детективний сюжет. Ось перший приклад: ромб має діагоналі 10 см і 24 см. Половини – 5 см і 12 см. Сторона a = √(25 + 144) = √169 = 13 см. Периметр – 52 см. Просто, але елегантно, правда?
Інший сценарій: площа ромба 48 см², одна діагональ 12 см. Знаходимо другу: d2 = (2 × S) / d1 = 96 / 12 = 8 см. Потім a = √((6)^2 + (4)^2) = √(36 + 16) = √52 ≈ 7.21 см. P ≈ 28.84 см. Тут ми поєднуємо площу з периметром, показуючи зв’язок фігур.
Для просунутих: ромб вписаний у коло з радіусом 5 см (відстань від центру до вершини). Сторона залежить від кута, але якщо це квадрат, a = 5√2 ≈ 7.07 см, P ≈ 28.28 см. Такі приклади розширюють горизонти, роблячи геометрію живою.
- Задача з кутами: якщо кут 45°, а діагональ 10 см, знайдіть сторону через тригонометрію – a = d1 / (√2), але це для квадрата; загалом використовуйте sin і cos.
- Комбінована: ромб з периметром 40 см, знайдіть сторону – a = 10 см, просто, але додає перевірку.
- Реальна: у паркету ромбова плитка зі стороною 15 см, скільки метрів кромки для 10 плиток? P однієї = 60 см, для 10 – 6 м, але з урахуванням стиків.
Ці приклади не тільки ілюструють формули, але й показують, як ромб вплітається в повсякденність, від шкільних зошитів до будівельних креслень.
Застосування периметру ромба в реальному житті
Ромби оточують нас скрізь, наче невидимі каркаси світу. У архітектурі вони формують дахи, де периметр визначає довжину балок – уявіть будинок з ромбовими вікнами, де точний розрахунок економить матеріали. У дизайні ювелірних виробів ромб – основа для кулонів, і знання периметру допомагає врізати золото без втрат.
У спорті, як у бейсбольному полі, ромб – це інфілд, де периметр впливає на стратегію бігу. Навіть у природі, у кристалах солі чи сніжинках, ромбові форми вимагають розуміння периметру для наукових моделей. А в комп’ютерній графіці обчислення периметру ромба – ключ до рендерингу 3D-моделей, де помилка в пікселях руйнує ілюзію.
Сучасні приклади з 2025 року: у екологічному дизайні ромбові сонячні панелі оптимізуються за периметром для максимальної ефективності, як у проєктах на базі даних з houseofmath.com. Це робить геометрію не просто теорією, а інструментом для інновацій.
Типові помилки при обчисленні периметру ромба
Навіть досвідчені математики іноді спотикаються об прості пастки, тож ось добірка поширених помилок з порадами, як їх уникнути. 😊
- Змішування периметру з площею: Багато хто плутає P = 4a з S = (d1 × d2)/2, додаючи діагоналі замість множення сторони. Перевіряйте, що ви рахуєте саме сумарну довжину сторін. 😅
- Ігнорування рівності сторін: Якщо фігура не ромб, а паралелограм з нерівними сторонами, формула не спрацює – завжди підтверджуйте, що всі сторони рівні. 🤔
- Помилки з діагоналями: Забувають ділити діагоналі навпіл перед Піфагором, отримуючи завищену сторону. Завжди halves! 🔍
- Округлення на ранніх етапах: Якщо a = √(13), не округлюйте до 3.6 одразу – помножте 4 × √13 ≈ 14.42 точно. 📏
- Неврахування одиниць: Сантиметри в метри – плутанина призводить до абсурдних результатів, як 20 см замість 0.2 м. Перевіряйте шкалу! ⚠️
Уникаючи цих помилок, ви робите обчислення надійними, наче добре налаштований механізм. 😌
Розширені методи: периметр через кути та тригонометрію
Коли в грі кути, ромб перетворюється на поле для тригонометрії. Якщо відомий кут α і діагональ d1, сторона a = (d1 / 2) / sin(α/2), але частіше використовують cos чи sin для повного розрахунку. Наприклад, для α = 60°, d1 = 10 см: половина d1 = 5 см, a = 5 / sin(30°) = 5 / 0.5 = 10 см. Потім P = 40 см.
Це додає глибини, особливо в задачах з векторами чи координатами. У координатній площині ромб з вершинами (0,0), (a,0), (a+b,c), (b,c) дозволяє знайти сторони через відстані, а периметр – сумуючи. Такі методи корисні в програмуванні, де алгоритми моделюють фігури.
У 2025 році, з розвитком AI в геометрії, ці методи інтегруються в додатки, як онлайн-калькулятори на onlinemschool.com, роблячи обчислення миттєвими, але розуміння основ залишається ключем.
Історичний погляд на ромб і його периметр
Ромб відомий з античності, коли Евклід у “Початках” описував його властивості, хоч і не називав саме так. У середньовіччі ромби використовували в мозаїках, де периметр визначав рамки візерунків. Сьогодні, у цифрову еру, ромб – основа для алгоритмів у графіці, де формули периметру оптимізують рендеринг.
Цікаво, як ромб еволюціонував: від простих фігур у грецькій геометрії до складних моделей у фізиці, де периметр впливає на опір матеріалів. Це робить тему вічною, наче сама математика.
У культурному контексті ромб символізує баланс у багатьох традиціях, від африканських тканин до європейських гербів, де обчислення периметру – не просто математика, а спосіб зрозуміти гармонію.