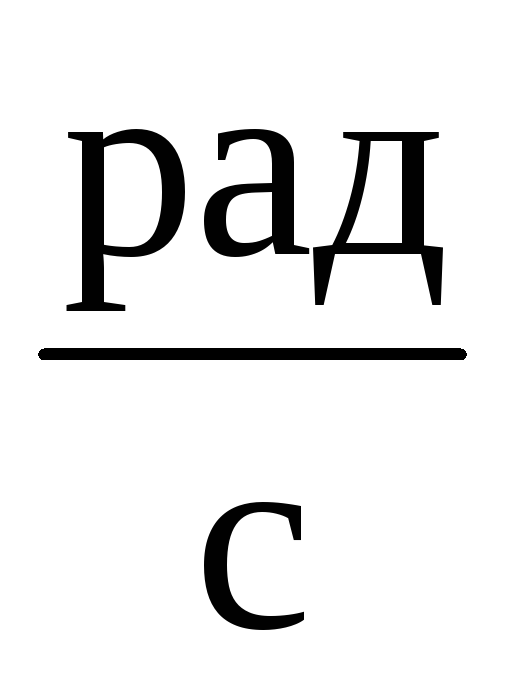Ви коли-небудь замислювалися, як вимірюють швидкість обертання — від колеса велосипеда до планет у космосі? Одиниця вимірювання кутової швидкості — це не просто термін із підручника, а ключ до розуміння руху, що оточує нас щодня! У цій статті ми розберемося, яка одиниця тут головна, як вона працює і чому вона важлива для науки й життя.
Це не нудна фізика — це захоплива подорож у світ обертів і чисел! Ми додамо яскравих фактів, детальних списків і зручних таблиць, щоб ви відчули ритм кутової швидкості. Готуйтеся до цікавого занурення!
Яка одиниця вимірювання кутової швидкості?
Основною одиницею вимірювання кутової швидкості в системі СІ є радіан за секунду, або скорочено рад/с. Це звучить трохи загадково, але насправді все просто: вона показує, на скільки радіанів об’єкт повертається за одну секунду. Один радіан — це кут, приблизно 57,3 градуса, а повне коло — це 2π радіанів, тобто близько 6,28.
Уявіть колесо, що крутиться: якщо воно робить один повний оберт (2π радіанів) за секунду, його кутова швидкість — 6,28 рад/с. Ця одиниця — як універсальний вимірювач для будь-якого обертання, від вентиляторів до зірок! Вона стала стандартом завдяки своїй зручності в математиці й фізиці.
Чому саме радіани? Бо вони “дружать” із формулами, роблячи обчислення чистими й елегантними. Рад/с — це не просто цифра, а справжній герой руху!
Як розраховують кутову швидкість?
Щоб зрозуміти одиницю вимірювання кутової швидкості, давайте розберемо, як її обчислюють. Це не складно — це захопливо! Ось основні кроки:
- Формула: Кутова швидкість (ω) = кут повороту (θ) / час (t), тобто ω = θ/t.
- Одиниці: Кут у радіанах ділиться на секунди — результат у рад/с.
- Приклад: Якщо колесо повертається на π радіанів (половина кола) за 2 секунди, то ω = π/2 = 1,57 рад/с.
- Зв’язок із обертанням: Один оберт за секунду = 2π рад/с — просто і красиво!
Ці кроки — як танець чисел! Рад/с дозволяє нам виміряти швидкість обертання легко й точно.
Чому саме радіан за секунду?
Радіан за секунду — не випадковий вибір, а продумане рішення науки! У системі СІ радіани — це природна одиниця для кутів, бо вони пов’язані з довжиною кола: довжина дуги дорівнює радіусу, помноженому на кут у радіанах. Це робить рад/с ідеальним для фізичних формул.
Порівняно з градусами за секунду, рад/с зручніший у математиці: немає зайвих коефіцієнтів при обчисленнях прискорення чи моменту сили. Наприклад, у рівнянні кутового прискорення (α = Δω/Δt) радіани спрощують усе до чистої краси. Це як мова, якою розмовляє природа!
Ця одиниця — як ключ до гармонії руху. Вона об’єднує теорію й практику, роблячи кутову швидкість зрозумілою і точною!
Альтернативні одиниці кутової швидкості
Хоча рад/с — головна одиниця, є й інші способи вимірювати кутову швидкість. Ось її “родичі”, які іноді з’являються в житті:
- Градуси за секунду (°/с): Звичні для повсякденності — 360°/с = один оберт за секунду.
- Оберти за секунду (об/с): Проста одиниця — 1 об/с = 2π рад/с, популярна в техніці.
- Оберти за хвилину (об/хв): Часто вживається для двигунів — 60 об/хв = 1 об/с = 6,28 рад/с.
Ці альтернативи — як різні діалекти однієї мови. Але рад/с залишається “офіційною” завдяки своїй універсальності!
Де використовують кутову швидкість?
Одиниця вимірювання кутової швидкості, рад/с, — це не просто абстракція, а робочий інструмент у багатьох сферах! Вона допомагає інженерам проектувати двигуни, астрономам вивчати рух планет, а фізикам розгадувати закони природи. Це число, що рухає світ!
Уявіть: швидкість обертання турбіни в літаку, колеса автомобіля чи навіть каруселі в парку — усе це можна виразити в рад/с. У космосі кутова швидкість Землі (близько 7,27 × 10⁻⁵ рад/с) визначає зміну дня і ночі. Це одиниця, що об’єднує мікро- і макросвіт!
Рад/с — як невидимий диригент обертального ритму. Вона всюди, де є рух і життя!
Таблиця: приклади кутової швидкості в житті
Щоб відчути, як працює рад/с, ось таблиця з реальними прикладами. Подивіться, де ховається кутова швидкість!
| Об’єкт | Кутова швидкість (рад/с) | Опис |
|---|---|---|
| Колесо велосипеда | ~10 рад/с | При швидкості 20 км/год |
| Вентилятор | ~100 рад/с | На середній швидкості |
| Земля | 7,27 × 10⁻⁵ рад/с | Один оберт за 24 години |
Ця таблиця — як віконце в світ обертів! Рад/с показує, як різноманітно рухається наше життя.
Як пов’язані кутова і лінійна швидкість?
Кутова швидкість у рад/с тісно дружить із лінійною швидкістю (метри за секунду), і це відкриває ще одну грань її краси! Формула проста: лінійна швидкість (v) = кутова швидкість (ω) × радіус (r), або v = ωr. Радіани тут — ідеальний “місток” між обертанням і рухом по прямій.
Наприклад, якщо колесо радіусом 0,5 м крутиться зі швидкістю 10 рад/с, то точка на його ободі рухається зі швидкістю 5 м/с. Це зв’язок, що допомагає інженерам розраховувати швидкість машин, а спортсменам — оберти дисків чи коліс!
Рад/с — це не просто одиниця, а провідник між двома світами руху. Її магія — у простоті й універсальності!
Цікаві факти про кутову швидкість
Одиниця вимірювання кутової швидкості ховає кілька сюрпризів! Ось факти, що роблять рад/с ще цікавішою:
- Безрозмірність: Радіан — умовна одиниця, тому рад/с технічно “чиста” величина в секундах⁻¹.
- Космос: Кутова швидкість пульсарів може сягати тисяч рад/с!
- Історія: Радіани ввели в 18 столітті, щоб спростити обчислення.
Ці факти — як маленькі перлини знань! Рад/с дивує своєю глибиною й історією.
Чому рад/с важлива для нас?
Одиниця вимірювання кутової швидкості, рад/с, — це не просто інструмент для фізиків, а частина нашого світу! Вона допомагає створювати технології — від пральних машин до космічних кораблів. Завдяки їй ми розуміємо, як рухаються планети й чому гвинт літака літає.
Для звичайної людини рад/с — це невидима нитка, що пов’язує повсякденність із наукою. Кожного разу, коли ви крутите кермо чи запускаєте дзиґу, ви торкаєтеся її магії!
Рад/с — це більше, ніж одиниця. Це ритм обертання, що пульсує в усьому, що нас оточує!